Link
Understanding Map Projections
Search

Coordinate Reference Systems

Now I’m going to complicate things a bit by introducing the term coordinate reference system (CRS), of which projections are a part.

Let’s break down the term a bit.

You may all be familiar with a coordinate system from your algebra days. A coordinate system defines a location in 2-dimensional space on an XY axis.

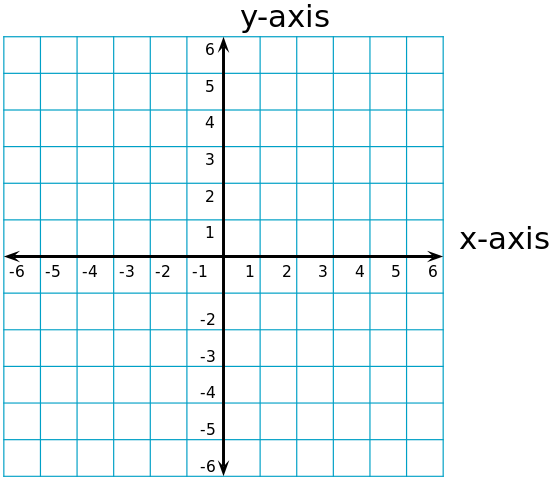
Cartesian coordinates
A two dimensional grid with an x and y axis. (c) Limaner , Public Domain.

 

So, what’s the problem?

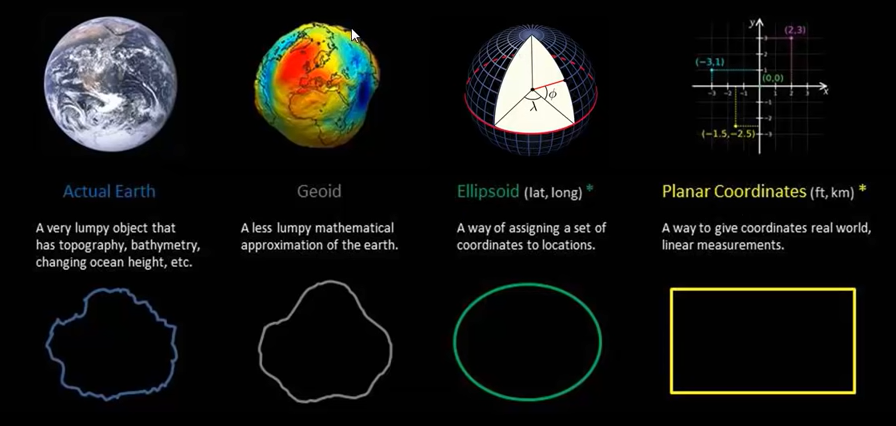
We live on a 3-dimensional earth that is neither perfectly round nor perfectly spherical.

  • The shape of the earth is mathematically approximated by something called a geoid, which tries to account for the irregularity of the earth’s surface.

  • An ellipsoid is a smooth-surfaced sphere, onto which we can assign coordinates to specific locations, reflected in degrees of latitude and longitude.

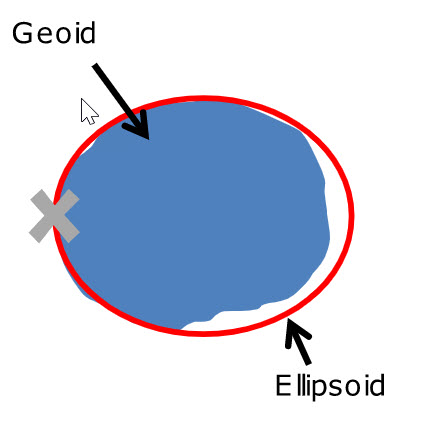
Geoid
A datum aligns a geoid with the ellipsoid at a particular location. (c) Manuel Gimond, CC BY-NC 4.0.

 

So we need a coordinate system that adapts to the Earth’s shape.

geoidEllipsoid
Understanding geoids and ellipsoids. (c) Rhumb Line Maps.

 

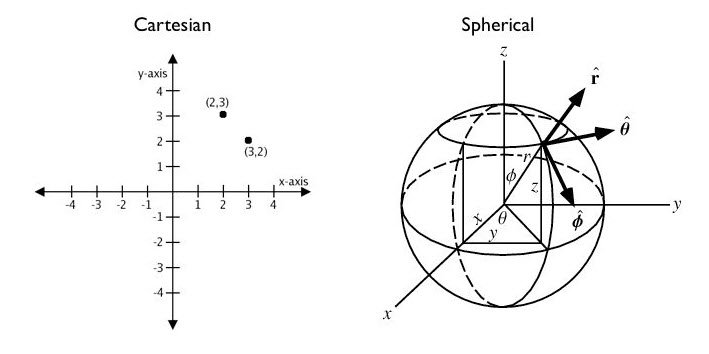
A CRS does this by defining the translation between a location on the earth and that location on a flattened, 2 dimensional coordinate system.

A CRS comprises:

  • Coordinate system: XY grid
  • Horizontal and vertical units: units used to define the grid along XY(and Z) axis
  • Datum: A model of the earth
  • Projection: mathematical equation used to flatten the surface of the earth onto a 2-dimensional plane , i.e. a paper map or a computer screen.
cartesianSpherical
Cartesian versus spherical, or geographic, coordinates. PostGIS.

 

At this point you might be wondering what a datum is. We’ll address this in the next section before we go on to talk about two different kinds of coordinate systems used in geospatial software.

This section references ideas, phrases, and images from Earth Lab, pbc GIS, Intro to GIS and Spatial Analysis, PostGIS and ArcGIS Blog.

Table of contents