2.2 Reading and Manipulating Tabular Data

Questions we’ll cover

• What are libraries?
• How do I use functions from libraries?
• How do I define a path to a data file relative to my code file?
• How can I read, manipulate, and analyze tabular data files in Python?

---

---

Words are useful, but what’s more useful are the sentences and stories we build with them. Similarly, while a lot of powerful, general tools are built into Python, specialized tools built up from these basic units live in libraries that can be called upon when needed.

Loading data into Python

To begin processing the exhibit-visit data, we need to load it into Python. We can do that using a library called NumPy, which stands for Numerical Python. In general, you should use this library when you want to do fancy things with lots of numbers, especially if you have matrices or arrays. To tell Python that we’d like to start using NumPy, we need to import it:

import numpy

Importing a library is like getting a piece of lab equipment out of a storage locker and setting it up on the bench. Libraries provide additional functionality to the basic Python package, much like a new piece of equipment adds functionality to a lab space. Just like in the lab, importing too many libraries can sometimes complicate and slow down your programs - so we only import what we need for each program.

Once we’ve imported the library, we can ask the library to read our data file for us:

data = numpy.loadtxt(fname='exhibit-visits-01.csv', delimiter=',')

These data correspond to the number of visitors to a digital museum exhibit that was shown in museums across Canada. The rows are the individual museums, and the columns are the daily number of visitors to the exhibit.

The expression numpy.loadtxt(...) is a function call that asks Python to run the function loadtxt which belongs to the numpy library. The dot notation in Python is used most of all as an object attribute/property specifier or for invoking its method. object.property will give you the object.property value, object_name.method() will invoke on object_name method.

As an example, John Smith is the John that belongs to the Smith family. We could use the dot notation to write his name smith.john, just as loadtxt is a function that belongs to the numpy library.

numpy.loadtxt has two parameters: the name of the file we want to read and the delimiter that separates values on a line. These both need to be character strings (or strings for short), so we put them in quotes.

This statement doesn’t produce any output because we’ve assigned the output to the variable data. If we want to check that the data have been loaded, we can print the variable’s value:

print(data)

[[ 6. 13. 11. ...  8.  4.  7.]
 [18.  4. 12. ...  2.  3.  4.]
 [19. 14. 12. ...  5.  6.  2.]
 ...
 [ 9. 10. 15. ...  6.  6.  4.]
 [ 8. 13. 18. ...  8.  6.  6.]
 [ 6. 18. 11. ...  8.  5.  5.]]

By default, only a few rows and columns are shown (with ... to omit elements when displaying big arrays). Note that, to save space when displaying NumPy arrays, Python does not show us trailing zeros, so 1.0 becomes 1..

Now that the data are in memory, we can manipulate them. First, let’s ask what type of thing data refers to:

print(type(data))

<class 'numpy.ndarray'>

The output tells us that data currently refers to an N-dimensional array, the functionality for which is provided by the NumPy library.

Data type within the Numpy array

A Numpy array contains one or more elements of the same type. The type function will only tell you that a variable is a NumPy array but won’t tell you the type of thing inside the array. We can find out the type of the data contained in the NumPy array.

print(data.dtype)

float64

This tells us that the NumPy array’s elements are floating-point numbers.

With the following command, we can see the array’s shape:

print(data.shape)

(60, 40)

The output tells us that the data array variable contains 60 rows and 40 columns. When we created the variable data to store our exhibit-visit data, we did not only create the array; we also created information about the array, called members or attributes. This extra information describes data in the same way an adjective describes a noun. data.shape is an attribute of data which describes the dimensions of data. We use the same dotted notation for the attributes of variables that we use for the functions in libraries because they have the same part-and-whole relationship.

If we want to get a single number from the array, we must provide an index in square brackets after the variable name, just as we do in math when referring to an element of a matrix. Our exhibit-visit data has two dimensions, so we will need to use two indices to refer to one specific value:

print('first value in data:', data[0, 0])

first value in data: 0.0

print('middle value in data:', data[29, 19])

middle value in data: 8.0

The expression data[29, 19] accesses the element at row 30, column 20. While this expression may not surprise you, data[0, 0] might. Programming languages like Fortran, MATLAB and R start counting at 1 because that’s what human beings have done for thousands of years. Languages in the C family (including C++, Java, Perl, and Python) count from 0 because it represents an offset from the first value in the array (the second value is offset by one index from the first value). This is closer to the way that computers represent arrays (if you are interested in the historical reasons behind counting indices from zero, you can read Mike Hoye’s blog post). As a result, if we have an M×N array in Python, its indices go from 0 to M-1 on the first axis and 0 to N-1 on the second. It takes a bit of getting used to, but one way to remember the rule is that the index is how many steps we have to take from the start to get the item we want.

In the Corner

What may also surprise you is that when Python displays an array, it shows the element with index [0, 0] in the upper left corner rather than the lower left. This is consistent with the way mathematicians draw matrices but different from the Cartesian coordinates. The indices are (row, column) instead of (column, row) for the same reason, which can be confusing when plotting data.

Slicing data

An index like [30, 20] selects a single element of an array, but we can select whole sections as well. For example, we can select the first ten days (columns) of values for the first four museums (rows) like this:

print(data[0:4, 0:10])

[[ 6. 13. 11. 11.  7.  7.  4.  6.  8.  8.]
 [18.  4. 12.  5. 12.  7. 11.  5. 11.  3.]
 [19. 14. 12. 17.  7. 12. 11.  7.  4.  2.]
 [17.  4.  4.  7.  6. 15.  6.  4.  9. 11.]]

The slice 0:4 means, “Start at index 0 and go up to, but not including, index 4”. Again, the up-to-but-not-including takes a bit of getting used to, but the rule is that the difference between the upper and lower bounds is the number of values in the slice.

We don’t have to start slices at 0:

print(data[5:10, 0:10])

[[12.  5. 18.  9.  5.  3. 10.  3. 12.  7.]
 [ 9. 17. 15.  8.  9.  3. 13.  7.  8.  2.]
 [20.  8.  5. 13. 15. 10.  6. 10.  6.  7.]
 [ 6. 16. 12.  6.  8. 14.  6. 13. 10. 11.]
 [18. 15. 16. 14. 12.  7.  3.  8.  9. 11.]]

We also don’t have to include the upper and lower bound on the slice. If we don’t include the lower bound, Python uses 0 by default; if we don’t include the upper, the slice runs to the end of the axis, and if we don’t include either (i.e., if we use ‘:’ on its own), the slice includes everything:

small = data[:3, 36:]
print('small is:')
print(small)

The above example selects rows 0 through 2 and columns 36 through to the end of the array.

small is:
[[5. 8. 4. 7.]
 [5. 2. 3. 4.]
 [5. 5. 6. 2.]]

Analyzing data

NumPy has several useful functions that take an array as input to perform operations on its values. If we want to find the average visits for all museums on all days, for example, we can ask NumPy to compute data’s mean value:

print(numpy.mean(data))

7.437916666666666

mean is a function that takes an array as an argument.

Sidenote: Not All Functions Have Input

Generally, a function uses inputs to produce outputs. However, some functions produce outputs without needing any input. For example, checking the current time doesn’t require any input.

import time
print(time.ctime())

Tue Nov 18 21:06:59 2025

For functions that don’t take in any arguments, we still need parentheses (()) to tell Python to go and do something for us.

---

Let’s use three other NumPy functions to get some descriptive values about the dataset. We’ll also use multiple assignment, a convenient Python feature that will enable us to do this all in one line.

maxval, minval, stdval = numpy.amax(data), numpy.amin(data), numpy.std(data)

print('maximum visits:', maxval)
print('minimum visits:', minval)
print('standard deviation:', stdval)

Here we’ve assigned the return value from numpy.amax(data) to the variable maxval, the value from numpy.amin(data) to minval, and so on.

maximum visits: 20.0
minimum visits: 0.0
standard deviation: 4.315222550427987

Sidenote: Mystery Functions in IPython

How did we know what functions NumPy has and how to use them? If you are working in IPython, a Jupyter Notebook, and some text editors, there is an easy way to find out. If you type the name of something followed by a dot, then you can use tab-completion (e.g. type numpy. and then press Tab) to see a list of all functions and attributes that you can use.

Sidenote: Confusing Function Names

One might wonder why the functions are called amax and amin and not max and min or why the other is called mean and not amean. The package numpy does provide functions max and min that are fully equivalent to amax and amin, but they share a name with standard library functions max and min that come with Python itself. Referring to the functions like we did above, that is numpy.max for example, does not cause problems, but there are other ways to refer to them that could. In addition, text editors might highlight (color) these functions like standard library function, even though they belong to NumPy, which can be confusing and lead to errors. Since there is no function called mean in the standard library, there is no function called amean.

---

When analyzing data, though, we often want to look at variations in statistical values, such as the maximum visits per museum or the average visits per day. One way to do this is to create a new temporary array of the data we want, then ask it to do the calculation:

museum_0 = data[0, :] # 0 on the first axis (rows), everything on the second (columns)
print('maximum visits for museum 0:', numpy.amax(museum_0))

maximum visits for museum 0: 18.0

We don’t actually need to store the row in a variable of its own. Instead, we can combine the selection and the function call:

print("maximum visits for museum 2:", numpy.amax(data[2, :]))

maximum visits for museum 2: 19.0

What if we need the maximum visits for each museum over all days (as in the next diagram on the left) or the average for each day (as in the diagram on the right)? As the diagram below shows, we want to perform the operation across an axis:

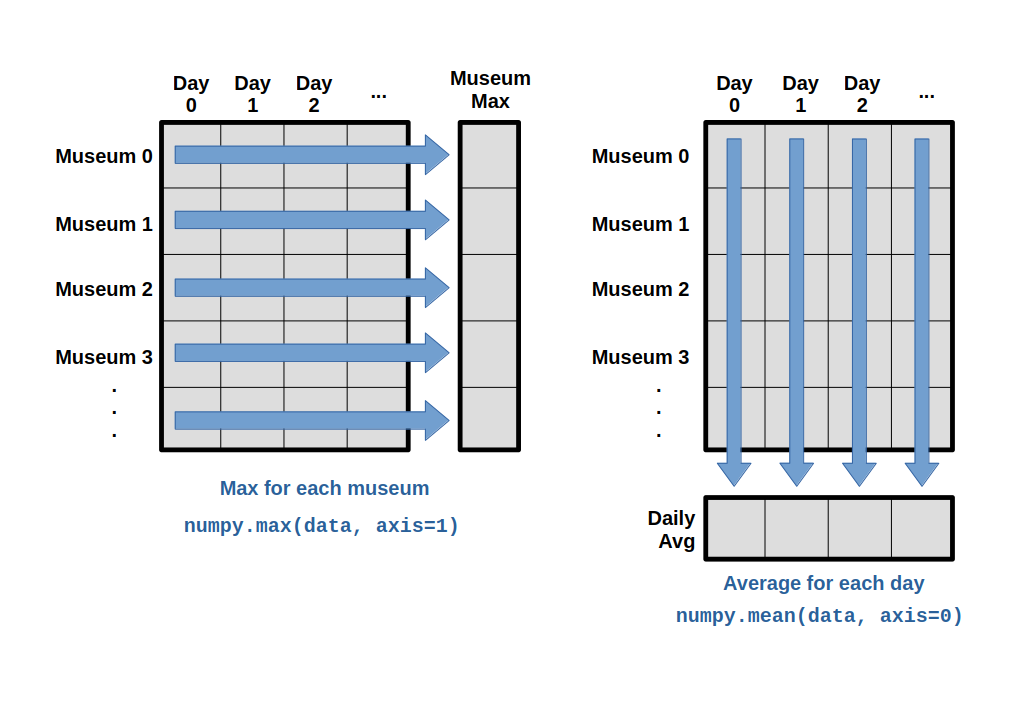
To find the maximum number of visits reported for each museum, you would apply the max function moving across the columns (axis 1). To find the daily average number of visits reported across museums, you would apply the mean function moving down the rows (axis 0).

To support this functionality, most array functions allow us to specify the axis we want to work on. If we ask for the max across axis 1 (columns in our 2D example), we get:

print(numpy.max(data, axis=1))

[18. 18. 19. 18. 17. 18. 17. 20. 17. 18. 18. 18. 17. 16. 14. 18. 19. 19.
 15. 19. 19. 18. 17. 16. 17. 17. 18. 17. 20. 17. 16. 19. 15. 18. 19. 17.
 16. 17. 19. 16. 18. 19. 16. 19. 18. 16. 19. 15. 16. 18. 14. 20. 19. 15.
 19. 19. 17. 19. 18. 18.]

As a quick check, we can ask this array what its shape is. We expect 60 museum maximums:

print(numpy.max(data, axis=1).shape)

(60,)

The expression (60,) tells us we have an N×1 vector, so this is the maximum visits per day for each museum.

If we ask for the average across/down axis 0 (rows in our 2D example), we get:

print(numpy.mean(data, axis=0))

[13.25       11.96666667 11.03333333 10.16666667 10.          8.66666667
  9.15        7.25        7.33333333  6.58333333  6.06666667  5.95
  5.11666667  3.6         3.3         3.56666667  2.48333333  1.5
  3.8         5.23333333  5.95        8.36666667 11.56666667 12.35
 11.96666667 11.03333333 10.16666667 10.          8.66666667  9.58333333
  9.15        8.35        7.25        6.58333333  6.06666667  5.95
  5.86666667  5.23333333  3.8         3.6       ]

Check the array shape. We expect 40 averages, one for each day of the study:

print(numpy.mean(data, axis=0).shape)

(40,)

Similarly, we can apply the mean function to axis 1 to get the museum’s average visits over the duration of the exhibit (60 values).

print(numpy.mean(data, axis=1))

[7.275 6.65  7.05  6.875 6.95  6.825 7.    7.925 8.075 8.475 8.075 6.975
 7.15  7.225 6.525 8.075 8.25  7.3   6.75  8.175 6.85  7.425 7.    7.3
 7.1   6.95  6.925 7.3   7.45  8.45  7.275 7.825 8.    7.975 8.325 6.975
 6.9   8.4   6.225 6.725 7.225 7.275 7.45  6.9   7.95  7.75  8.25  7.25
 6.925 7.3   7.325 7.4   8.475 6.7   8.45  6.85  7.65  8.05  8.725 7.4  ]

Challenge: Slicing Strings

A section of an array is called a slice. We can take slices of character strings as well:

element = 'oxygen'
print('first three characters:', element[0:3])
print('last three characters:', element[3:6])

first three characters: oxy
last three characters: gen

Ask yourself: What is the value of element[:4]? What about element[4:]? Or element[:]?

Solution

oxyg
en
oxygen

Ask yourself: What is element[-1]? What is element[-2]?

Solution

n
e

Ask yourself: Given those answers, explain what element[1:-1] does

Solution

Creates a substring from index 1 up to (not including) the final index, effectively removing the first and last letters from ‘oxygen’

Ask yourself: How can we rewrite the slice for getting the last three characters of element,so that it works even if we assign a different string to element?

Test your solution with the following strings: carpentry, clone, hi.

Solution

element = 'oxygen'
print('last three characters:', element[-3:])
element = 'carpentry'
print('last three characters:', element[-3:])
element = 'clone'
print('last three characters:', element[-3:])
element = 'hi'
print('last three characters:', element[-3:])

last three characters: gen
last three characters: try
last three characters: one
last three characters: hi

---

Challenge: Thin Slices

The expression element[3:3] produces an empty string, i.e., a string that contains no characters. If data holds our array of ehibit-visit data, what does data[3:3, 4:4] produce? What about data[3:3, :]?

Solution

array([], shape=(0, 0), dtype=float64)
array([], shape=(0, 40), dtype=float64)

---

Challenge: Stacking Arrays

Arrays can be concatenated and stacked on top of one another, using NumPy’s vstack and hstack functions for vertical and horizontal stacking, respectively.

import numpy

A = numpy.array([[1, 2, 3], [4, 5, 6], [7, 8, 9]])
print('A = ')
print(A)

B = numpy.hstack([A, A])
print('B = ')
print(B)

C = numpy.vstack([A, A])
print('C = ')
print(C)

A =
[[1 2 3]
 [4 5 6]
 [7 8 9]]
B =
[[1 2 3 1 2 3]
 [4 5 6 4 5 6]
 [7 8 9 7 8 9]]
C =
[[1 2 3]
 [4 5 6]
 [7 8 9]
 [1 2 3]
 [4 5 6]
 [7 8 9]]

Write some additional code that slices the first and last columns of A, and stacks them into a 3x2 array. Make sure to print the results to verify your solution.

Solution

A ‘gotcha’ with array indexing is that singleton dimensions are dropped by default. That means A[:, 0] is a one dimensional array, which won’t stack as desired. To preserve singleton dimensions, the index itself can be a slice or array. For example, A[:, :1] returns a two dimensional array with one singleton dimension (i.e. a column vector).

D = numpy.hstack((A[:, :1], A[:, -1:]))
print('D = ')
print(D)

D =
[[1 3]
 [4 6]
 [7 9]]

Solution

An alternative way to achieve the same result is to use Numpy’s delete function to remove the second column of A. If you’re not sure what the parameters of numpy.delete mean, use the help files.

D = numpy.delete(arr=A, obj=1, axis=1)
print('D = ')
print(D)

D =
[[1 3]
 [4 6]
 [7 9]]

---

Challenge: Change In Number of Visits

The exhibit-visit data is longitudinal in the sense that each row represents a series of observations relating to one museum. This means that the change in visits over time is a meaningful concept. Let’s find out how to calculate changes in the data contained in an array with NumPy.

The numpy.diff() function takes an array and returns the differences between two successive values. Let’s use it to examine the changes each day across the first week of museum 3 from our exhibit-visit dataset.

museum3_week1 = data[3, :7]
print(museum3_week1)

[17.  4.  4.  7.  6. 15.  6.]

Calling print(numpy.diff(museum3_week1)) would do the following calculations

[4 - 17, 4 - 4, 7 - 4, 6 - 7, 15 - 6, 6 - 15]

and return the 6 difference values in a new array.

print(numpy.diff(museum3_week1))

[-13.   0.   3.  -1.   9.  -9.]

Note that the array of differences is shorter by one element (length 6).

When calling numpy.diff with a multi-dimensional array, an axis argument may be passed to the function to specify which axis to process.

Ask yourself: When applying numpy.diff to our 2D exhibit-visit array data, which axis would we specify?

Since the row axis (0) is museums, it does not make sense to get the difference between two arbitrary museums. The column axis (1) is in days, so the difference is the change in number of visits – a meaningful concept.

print(numpy.diff(data, axis=1))

[[  7.  -2.   0. ...   3.  -4.   3.]
 [-14.   8.  -7. ...  -3.   1.   1.]
 [ -5.  -2.   5. ...   0.   1.  -4.]
 ...
 [  1.   5.  -5. ...   0.   0.  -2.]
 [  5.   5.  -1. ...   0.  -2.   0.]
 [ 12.  -7.  -2. ...   3.  -3.   0.]]

Ask yourself: If the shape of an individual data file is (60, 40) (60 rows and 40 columns), what would the shape of the array be after you run the diff() function and why?

The shape will be (60, 39) because there is one fewer difference between columns than there are columns in the data.

Ask yourself: How would you find the largest change in exhibit visits for each museum? Does it matter if the change in exhibit visits is an increase or a decrease?

By using the numpy.amax() function after you apply the numpy.diff() function, you will get the largest difference between days.

print(numpy.amax(numpy.diff(data, axis=1), axis=1))

[ 7.  8. 10. 11. 11. 13. 10. 10. 11. 10.  8.  8.  7.  8. 10. 13.  8. 11.
  9. 10.  8.  8.  9.  9.  8.  9.  8. 10.  7. 14. 12. 10.  7. 11. 12.  8.
 10. 12.  9. 12. 13.  7. 10. 13. 12. 12. 11.  9.  9. 13.  8. 13.  9.  7.
  7.  8. 10.  8.  8. 12.]

If exhibit-visit values decrease along an axis, then the difference from one element to the next will be negative. If you are interested in the magnitude of the change and not the direction, the numpy.absolute() function will provide that.

Notice the difference if you get the largest absolute difference between readings.

print(numpy.amax(numpy.absolute(numpy.diff(data, axis=1)), axis=1))

[ 7. 14. 13. 13. 13. 13. 10. 12. 11. 10. 13. 12. 10. 10. 10. 13. 12. 13.
  9. 13. 10.  9.  9.  9. 11. 13.  9. 13. 13. 14. 12. 13.  7. 11. 12. 13.
 10. 12. 10. 12. 13. 13. 11. 13. 13. 12. 12.  9.  9. 13.  8. 13. 13.  9.
  8. 11. 13.  8.  9. 12.]

---

Key Points

• Import a library into a program using import libraryname.
• Use the numpy library to work with arrays in Python.
• The expression array.shape gives the shape of an array.
• Use array[x, y] to select a single element from a 2D array.
• Array indices start at 0, not 1.
• Use low:high to specify a slice that includes the indices from low to high-1.
• Use # some kind of explanation to add comments to programs.
• Use numpy.mean(array), numpy.amax(array), and numpy.amin(array) to calculate simple statistics.
• Use numpy.mean(array, axis=0) or numpy.mean(array, axis=1) to calculate statistics across the specified axis.